Sub-problem 2d: Effects of a Signal on an Existing Coordinated System

Finding the optimal common cycle length can be achieved by using any of several traffic models that take all of the previously-identified factors into consideration. The HCM, however, does not include a methodology that can be used to make this determination. For the purposes of this discussion we will choose a 90-second cycle; this choice will accommodate a progression band through the intersections that is no smaller than the shortest arterial green phase, which, in this case is found at SH 8.

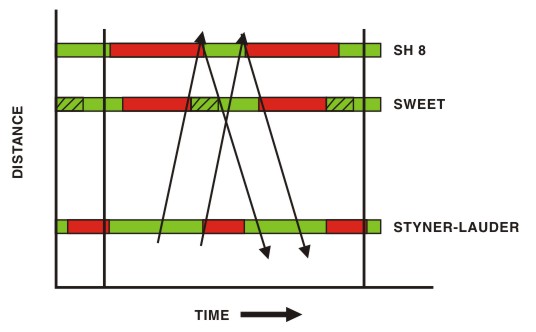
Now, if we extend the time–space diagram (see Exhibit 1-26) to include the new intersection at Styner-Lauder, we can determine the effect of a signal at this intersection on the entire coordinated system. Note that the distance to Styner-Lauder dictates an alternating relationship between the green phases with the adjacent intersection. Similarly, the close spacing of the SH 8 and Sweet intersections dictates a more-or-less simultaneous green phase strategy for the through movements. The simple two-phase operation at Styner-Lauder provides a longer green phase on the arterial (NB and SB approaches), so the additional signal is able to fit into the progression scheme without encroaching into the bands of progression that currently exist between the two signals. 

The conclusion that we can draw from this is that it is possible to signalize the Styner-Lauder intersection without a significant adverse effect on the driver-perceived progression, even though the arterial street analysis conducted in subproblem 2c suggests that travel speed will be impacted by 13 percent.

Exhibit 1-26. Signal Coordination Time/Space Diagram