Sub-problem 1b - Page 5 of 9

ID# C201B05

Sub-problem 1b: Maxwell Drive PM Peak Hour - With Conditions

Cycle Length Education
For a pre-timed signal, the standard equation for computing the minimum cycle length is:

(1)

where v_i is the volume for the critical movement in phase i, s_i is the saturation flow rate for the critical movement in phase i, N is the number of phases per cycle, and L is the lost time per phase.

For actuated signals with dual-ring controllers like the one we portrayed in Exhibit 2-11, it helps to expand Equation (1) into three equations. The first one computes the v/s ratio for sequential pairs of movements to the left and right of the middle barrier in the A and B rings:

(2)

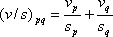Here pq takes on the values 1&2, 3&4, 5&6, and 7&8 corresponding to the four quadrants of the dual ring pattern.

The second equation computes the maximum v/s ratio for the left and right halves of the dual ring pattern:

(3)	(v/s)_L = max((v/s)₁₂,(v/s)₅₆) and (v/s)_R = max((v/s)₃₄, (v/s)₇₈)

The third equation takes the two results from Equation (3) and computes a minimum cycle length:

(4)

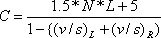This is the process being followed in the spreadsheet we used for the analysis.

Equations (2) through (4) show that Equation (1) can be obtained easily. First, realize that N equals 4. Second, see that the sequence of critical movements is either: 1,2,3,4; 1,2,7,8; 5,6,3,4; or 5,6,7,8. Third, notice that the sum of the v_i/s_i ratios identified in the denominator of Equation (1) is the same as the left and right half based sum shown in Equation (4).

Discussion:
In practice, we don't often use equations in the formal style they are presented here. The equations are helpful, though, because they are a shorthand-way of expressing ideas. You might check-out the spreadsheet and see if you can identify how equations (2), (3) and (4) have been implemented.

[ Back ] [ Continue ] to Critical Movement Techniques